Masih ingatkah anda dengan pelajaran Integral??
)^r.\;u'(x)}\;dx={\color{Red}&space;\frac&space;{1}{r+1}(u(x))^{r+1}+c}) di mana c adalah konstanta dan
di mana c adalah konstanta dan 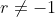
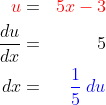
^4{\color{Blue}&space;dx}&=&\int&space;{\color{Red}&space;u}^4.{\color{Blue}&space;\frac&space;15\;du}\\&=&{\color{Blue}&space;\frac&space;15}.\frac{1}{4+1}.{\color{Red}&space;u}^{4+1}+C\\&=&\frac{1}{25}\;{\color{Red}&space;u}^5+C\\&=&\frac{1}{25}\;({\color{Red}&space;5x-3})^5+C\end{align*})
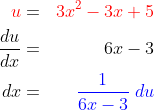
(3x^2-3x+5)^8\;dx&=&\int&space;(2x-1).{\color{Red}&space;u}^8\;{\color{Blue}&space;\frac{1}{6x-3}\;du}\\&=&\int&space;\frac{2x-1}{{\color{Blue}&space;3(2x-1)}}\;{\color{Red}&space;u}^8\;{\color{Blue}&space;du}\\&=&\int&space;\frac{1}{3}\;{\color{Red}&space;u}^8\;{\color{Blue}&space;du}\\&=&\frac&space;13.\frac{1}{8+1}.{\color{Red}&space;u}^{8+1}+C\\&=&\frac{1}{27}.{\color{Red}&space;u}^9&space;+C\\&=&\frac{1}{27}({\color{Red}&space;3x^2-3x+5})^9+C\end{align*})
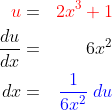
\sqrt{{\color{Red}&space;2x^3+1}}+C\end{align*})
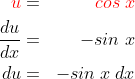
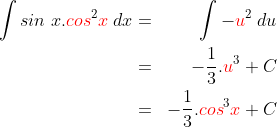
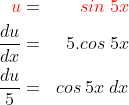
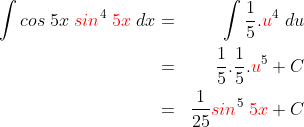
Yuuuuuuk belajar lagi…!!!!
Kali ini khusus kita bahas tentang integral subtitusi, contoh soal dan pembahasannya ok…!!!
Jangan sampai ketinggalan ya…
Jika u suatu fungsi yang dapat didiferensialkan dan r suatu bilangan rasional tak nol, maka
Nah…udah lihat rumus integral yang di atas sono tuh…???
Pusing,tidak..??? hehehe…lebih baik langsung di contohin aja ya….
contoh soal dan pembahasan integral subtitusi :
1. ^4dx=....)
Jawab :
* kita misalkan 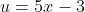 dan fungsi u dapat diturunkan menjadi
dan fungsi u dapat diturunkan menjadi
* Baru kita subtitusikan ke soal :
Jangan sampai lupa untuk mengembalikan permisalan kita 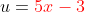 ya…..
ya…..
2. (3x^2-3x+5)^8\;dx=...)
Jawab :
* kita misalkan 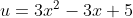 dan fungsi u dapat diturunkan menjadi :
dan fungsi u dapat diturunkan menjadi :
* Baru kita subtitusikan ke soal :
3. 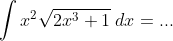
Jawab :
* kita misalkan 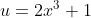 dan fungsi u dapat diturunkan menjadi
dan fungsi u dapat diturunkan menjadi
* Baru kita subtitusikan ke soal :
4. 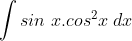 = …
= …
Jawab :
* kita misalkan 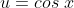 maka
maka
*sehingga :
5. 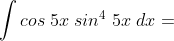 …
…
Jawab :
* kita misalkan 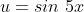 maka :
maka :
*sehingga :
Wheheheehe…latihan soal dan pembahasan integral subtitusi aljabar dan trigonometrinya dicukupkan dulu yaaaaaa….kapan-kapan ditambah lagi soalnya….
Selamat belajar ………..!!!!
Sumber : www.meetmath.com















3 comments
Pening....~x(
Banyak Belajar dan sering Latihan Soal pasti Bisa....:)
waw pusing nya ....
Posting Komentar
Silakan Tinggalkan pesan mengenai Blog ini, Tapi jangan Nyepam ya...Makasi atas Kunjunganya :)