Komposisi Fungsi
Komposisi fungsi merupakan penggabungan operasi dua fungsi secara berurutan yang akan menghasilkan sebuah fungsi baru.
Komposisi dua fungsi  dan
dan 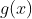 dinotasikan dengan simbol
dinotasikan dengan simbol 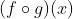 atau
atau 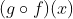 .
.
dimana
Sifat Komposisi Fungsi
Contoh :
diberikan fungsi :
1. 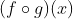 = ….?
= ….?
* fungsi 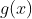 disubtitusikan ke fungsi
disubtitusikan ke fungsi 
2. 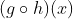 = ….?
= ….?
* fungsi 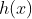 disubtitusikan ke fungsi
disubtitusikan ke fungsi 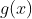
3.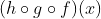 =…?
=…?
* fungsi  disubtitusikan terlebih dahulu ke fungsi
disubtitusikan terlebih dahulu ke fungsi 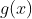 nah, hasilnya baru disubtitusikan ke fungsi
nah, hasilnya baru disubtitusikan ke fungsi 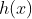 , perhatikan warna mewakili subtitusi ….ok!
, perhatikan warna mewakili subtitusi ….ok!
Bagaimana contoh diatas???sudah cukup jelas,kan???!!
Berhati-hatilah dalam mensubtitusikan ya….
Berhati-hatilah dalam mensubtitusikan ya….
Mencari salah satu fungsi jika komposisi fungsi diketahui
1. Mencari 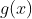 jika
jika  dan
dan 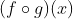 diketahui
diketahui
contoh soal dan pembahasan :
Diketahui 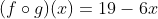 dan
dan 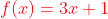 tentukan fungsi
tentukan fungsi 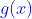 !
!
jawab :
2. Mencari  jika
jika 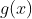 dan
dan 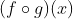 diketahui
diketahui
contoh soal dan pembahasan :
Diketahui 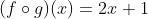 dan
dan 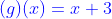 tentukan
tentukan 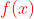 !
!
jawab :
Kita misalkan dulu :
Subtitusikan kembali ke fungsi :
Sumber : www.meetmath.com














.jpg)


1 comment
ane gak paham cara bacanya rumusnya mas, bisa dijelasin mas....
Posting Komentar
Silakan Tinggalkan pesan mengenai Blog ini, Tapi jangan Nyepam ya...Makasi atas Kunjunganya :)